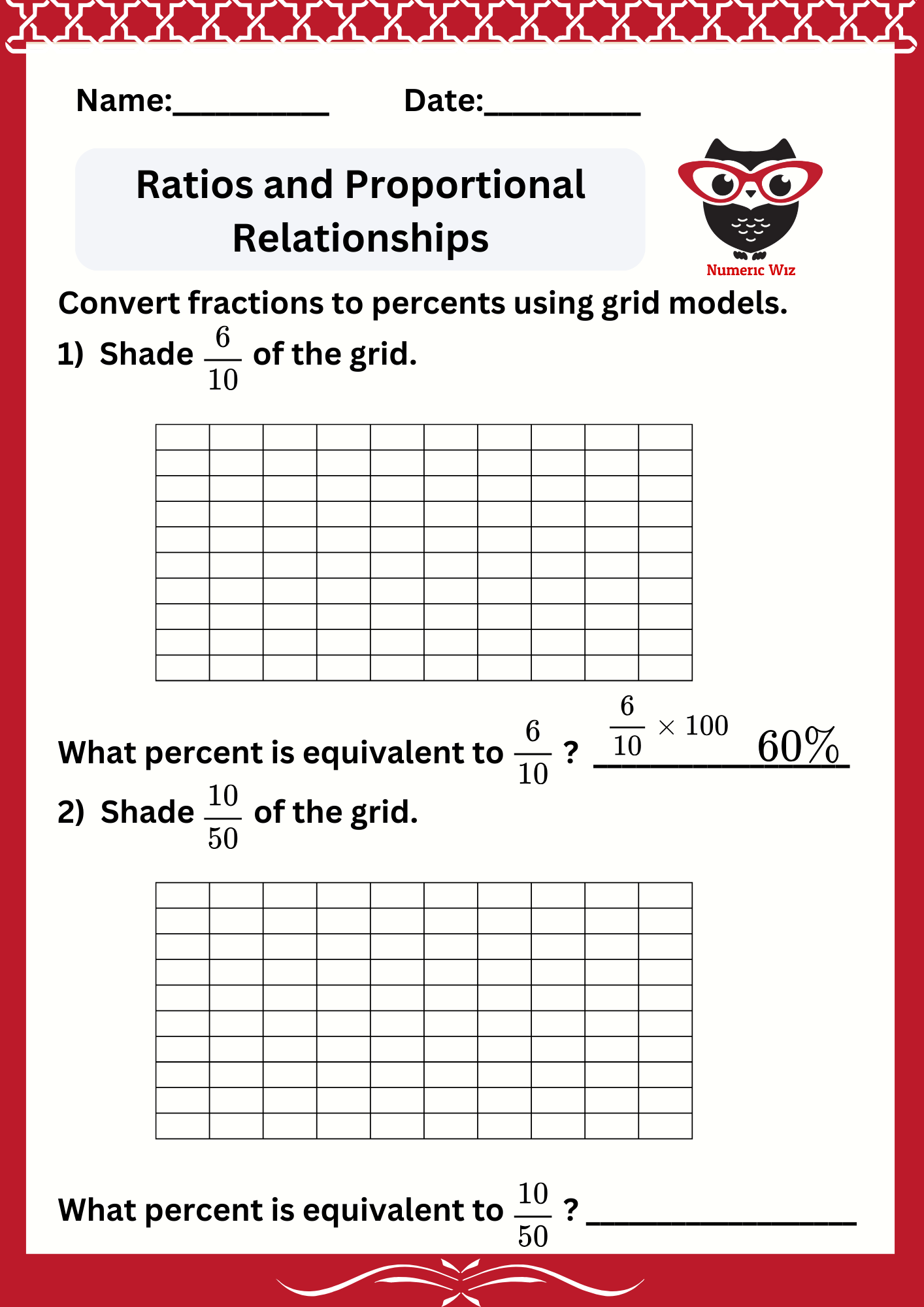
Understanding how to convert fractions into percent is a crucial math skill. By using grid models, you can visualize this process in a simple and effective way. This guide will help you learn the concept with clear explanations, examples, and practical applications.
A grid model is a visual representation that divides a square or rectangle into 100 equal parts. Each part represents 1% of the total. Grid models make it easier to see how fractions relate to percents by breaking the process into manageable steps.
Follow these steps to convert a fraction to a percent:
Understand the Fraction
A fraction has two parts: the numerator (top number) and the denominator (bottom number). For example, in3/4, the numerator is 3, and the denominator is 4.
Scale the Fraction to Denominator 100
To convert a fraction into a percent, rewrite the denominator as 100. Multiply both the numerator and denominator by the same number so that the denominator becomes 100.
For 3/4, multiply both parts by 25:
3/4=3×25/4×25=75/100
Visualize on the Grid
Shade 75 out of 100 squares on the grid to represent 75/100. This shaded area corresponds to 75%.
Write as a Percent
Once the fraction is expressed with a denominator of 100, the numerator becomes the percent. In this case, 75/100=75%
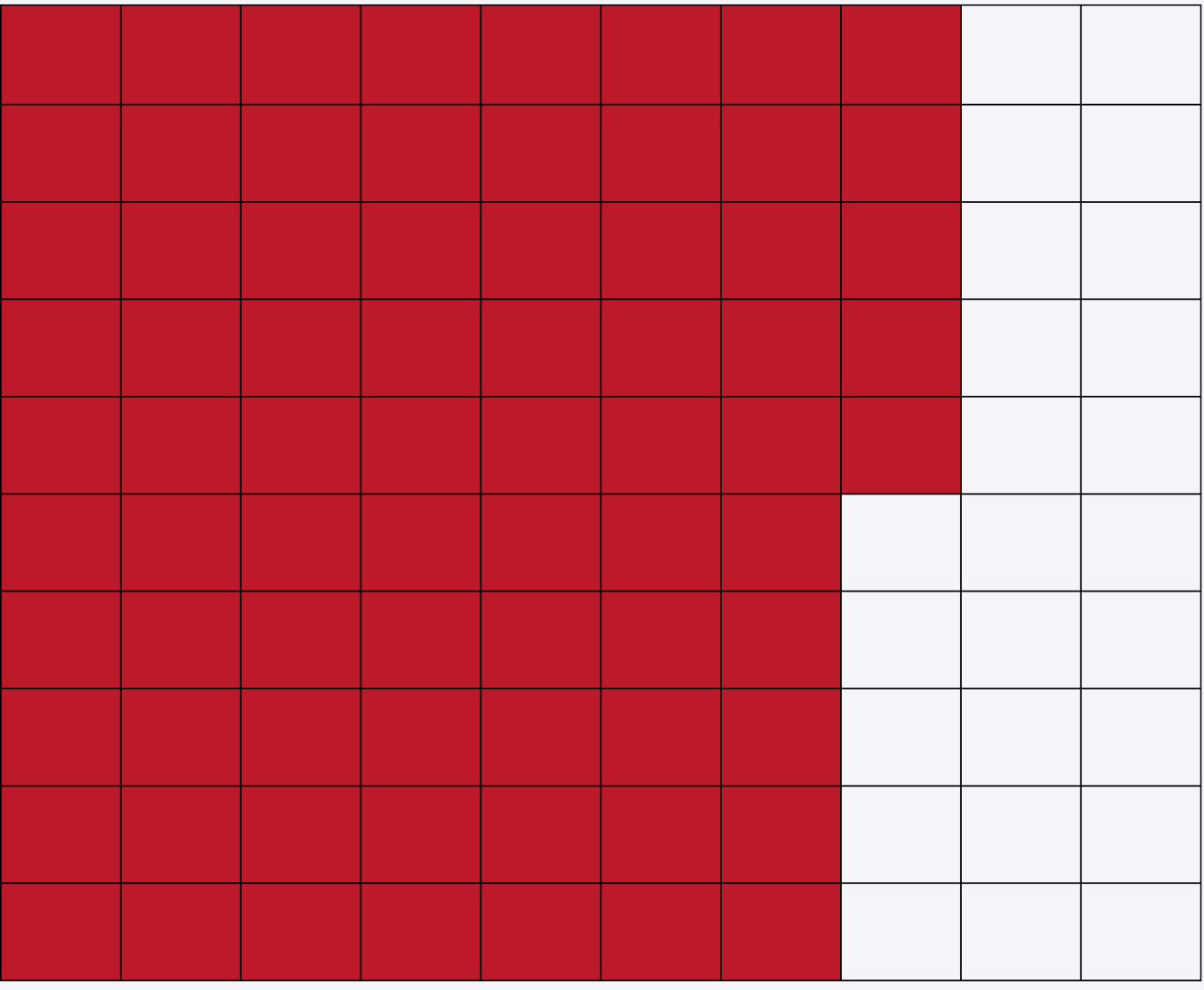
Example 1: Convert 2/5 to a Percent Using a Grid Model
Rewrite with Denominator 100:
Multiply both numerator and denominator by 20:
2/5=2×20/5×20=40/100
Visualize on the Grid:
Shade 40 out of 100 squares.
Conclusion:2/5 is equal to 40%.
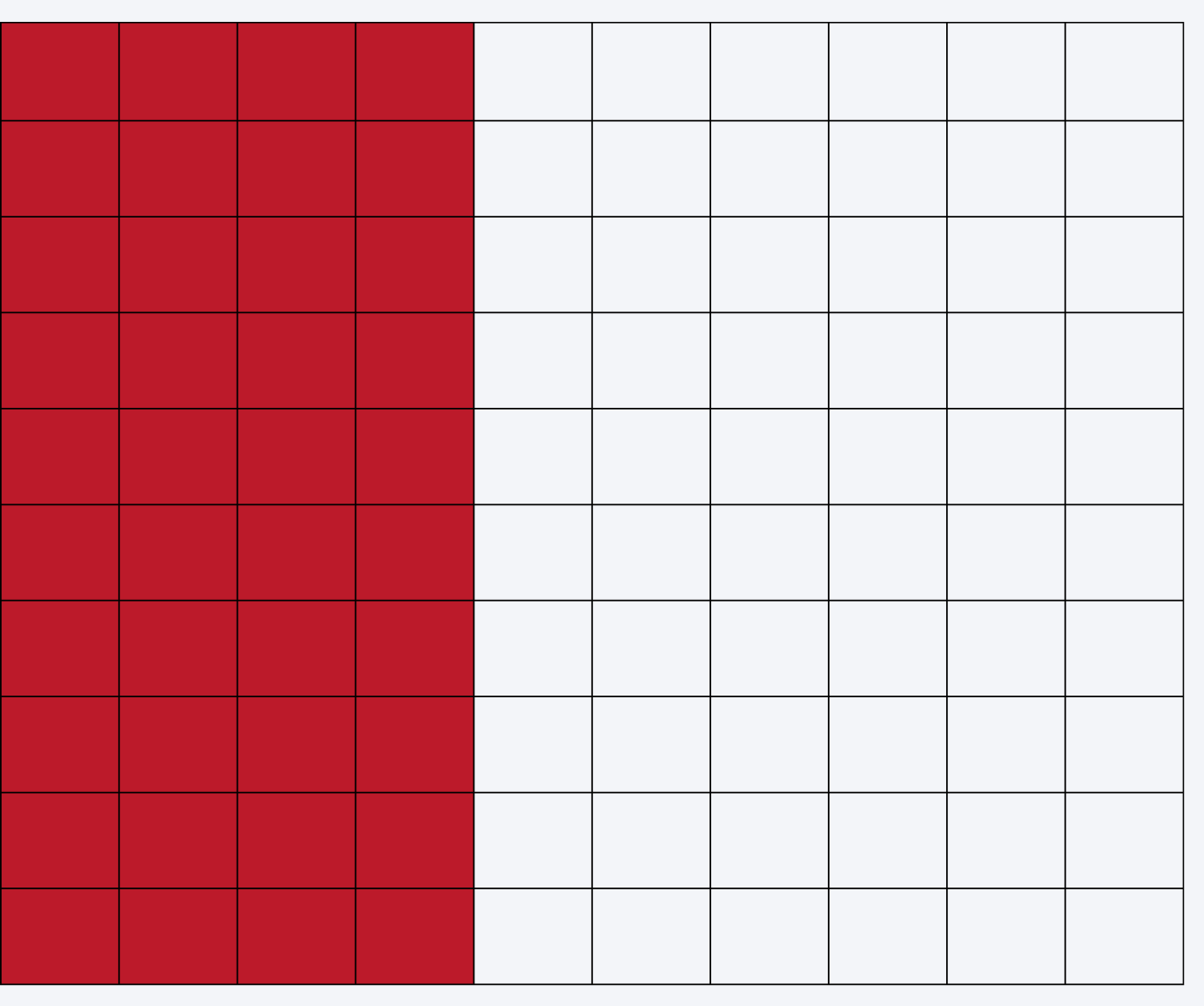
Example 2: Solve a Real-Life Problem
Question: A class of 30 students has 18 students who passed a math test. What percent of the class passed the test?
Write the Fraction:18/30
Simplify and Scale:
Simplify 18/30 to 3/5
Convert 3/5 to a denominator of 100:
3/5=3×20/5×20=60/100
Visualize on the Grid:
Shade 60 squares out of 100.

Conclusion:
60% of the class passed the test.
Simplifies Learning: The visual aspect of grid models makes abstract concepts easier to understand.
Builds Confidence: Students can see the relationship between fractions and percents, helping them tackle more complex problems with ease.
Applies to Real Life: Grasping this skill helps solve real-world problems, such as calculating discounts, tips, and success rates.
Mastering how to convert fractions to percents using grid models can transform your math skills. By combining visual learning and practical applications, you'll develop a strong foundation for solving percent problems with confidence!
Let's team up with NumericWiz to unlock the power of grid models and make converting fractions to percent easy and fun!
For a limited time
