Identify rational and irrational square roots

Standard: 8.NS.A.1

Know that numbers that are not rational are called irrational. Understand informally that every number has a decimal expansion; for rational numbers show that the decimal expansion repeats eventually, and convert a decimal expansion which repeats eventually into a rational number.

Learning Outcomes

Square roots of perfect squares are rational.
Square roots of non-perfect squares are irrational.
Rational square roots can be written as fractions or whole numbers.
Irrational square roots have non-repeating, non-terminating decimals

Download Identify rational and irrational square roots

Click the button below to get instant access to these premium worksheets for use in the classroom or at a home.

Identifying Rational and Irrational Square Roots

Numbers can be classified as rational or irrational, and understanding their square roots is essential in mathematics. Let’s explore how to identify whether a square root is rational or irrational!

What Are Rational and Irrational Numbers?

A rational number can be written as a fraction 𝑎 / 𝑏 where a and b are integers, and b ≠ 0. It has a terminating or repeating decimal expansion.

Examples:

3 / 4 = 0.75

1 / 3 = 0.333...

An irrational number cannot be written as a fraction. Its decimal never terminates and never repeats.

Examples: π = 3.141592653..., e = 2.718..., and √2 = 1.41421356...

Understanding Square Roots

The square root of a number x is a value that, when multiplied by itself, gives x. Some square roots are rational, while others are irrational.

Identifying Rational Square Roots

A square root is rational if it results in a whole number or a fraction. This happens when the number inside the square root is a perfect square (like 1, 4, 9, 16, 25, etc.).

Examples of Rational Square Roots:

If the square root of a number results in a whole number or a fraction, it is rational.

Identifying Irrational Square Roots

A square root is irrational if the number inside the square root is not a perfect square. In these cases, the decimal representation goes on forever without repeating.

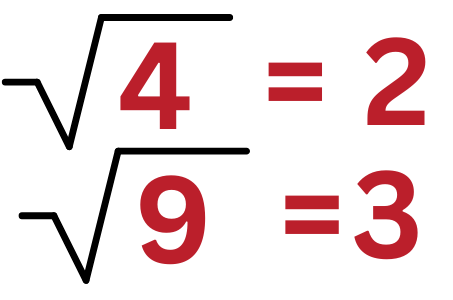
Example of Irrational Square Roots:

(decimal never repeats)

Since numbers like 2, 3, 5, and 7 are not perfect squares, their square roots cannot be written as fractions, making them irrational.

Key Takeaways:

Understanding rational and irrational square roots helps in algebra, geometry, and real-world applications like engineering and physics. Let’s explore and practice with the help of designed worksheets at NumericWiz!