Comparing and Ordering Rational & Irrational Numbers

Numbers are all around us, from measuring distances to calculating time. But not all numbers behave the same way! Some numbers, like fractions and whole numbers, are rational, while others, like π (pi) and √2, are irrational because they never end and never repeat. So, how do we compare and order these different types of numbers? Let’s explore!

What Are Rational and Irrational Numbers?

 Rational Numbers

A rational number is any number that can be written as a fraction a/b where a and b are integers, and b ≠ 0. This includes:

• Whole numbers (5, 12, 100)
• Fractions (½, ¾, 2/5)
• Decimals that terminate (end) or repeat (e.g., 0.75, 0.333..., 2.125)

 Irrational Numbers

Irrational numbers cannot be written as a fraction because their decimal form goes on forever without repeating. Examples include:

•  π ≈ 3.141592653... (never-ending, non-repeating)
•  √2 ≈ 1.414213... (square root of non-perfect squares)
•  e ≈ 2.7182818... (Euler’s number, used in logarithms)

How to Compare and Order Rational & Irrational Numbers?

Since irrational numbers don’t have exact values, we use rational approximations (rounded decimal values) to compare them with rational numbers.

Step 1: Convert Everything to Decimal Form

To compare numbers, we first express each as a decimal.

Example: Compare ¾, √2, and 1.5

¾ = 0.75 (rational)

√2 ≈ 1.414 (irrational)

1.5 = 1.5 (rational)

Now we can order them:

0.75 < 1.414 < 1.5

So, ¾ < √2 < 1.5.

 Step 2: Place the Numbers on a Number Line

A number line helps visualize where each number falls.

 Example: Order π, 2.7, and √8

Approximations:

π ≈ 3.14

2.7 (already in decimal form)

√8 ≈ 2.83

Number Line Representation:

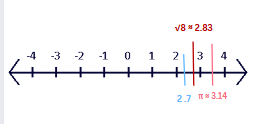
From left to right: 2.7 < √8 < π

Step 3: Compare Using Inequality Symbols

Once numbers are in decimal form and placed on the number line, we use < (less than) or > (greater than) symbols.

 Example: Compare 5/6, √3, and 0.8

Approximations:

5/6 = 0.8333...

√3 ≈ 1.732

0.8 (already in decimal form)

Now order them: 0.8 < 5/6 < √3

Written in inequality form:

0.8 < 5/6 < √3

Real-Life Applications of Comparing Rational & Irrational Numbers

This isn’t just math—it’s useful in real life!

Architecture & Engineering

Engineers compare square roots when calculating diagonal distances.

Builders estimate √2 and √3 when designing triangles and slopes.

Music & Sound Waves

Frequencies of musical notes often involve irrational numbers, affecting tuning and sound waves.

GPS & Navigation

GPS coordinates use irrational numbers like π to calculate distances and locations.

 Science & Physics

Scientists compare numbers like e and π in physics, chemistry, and astronomy.

By understanding how to compare and order rational and irrational numbers, we make sense of numbers beyond just whole numbers and fractions.

Let’s explore and practice with the help of designed Worksheets on  more!