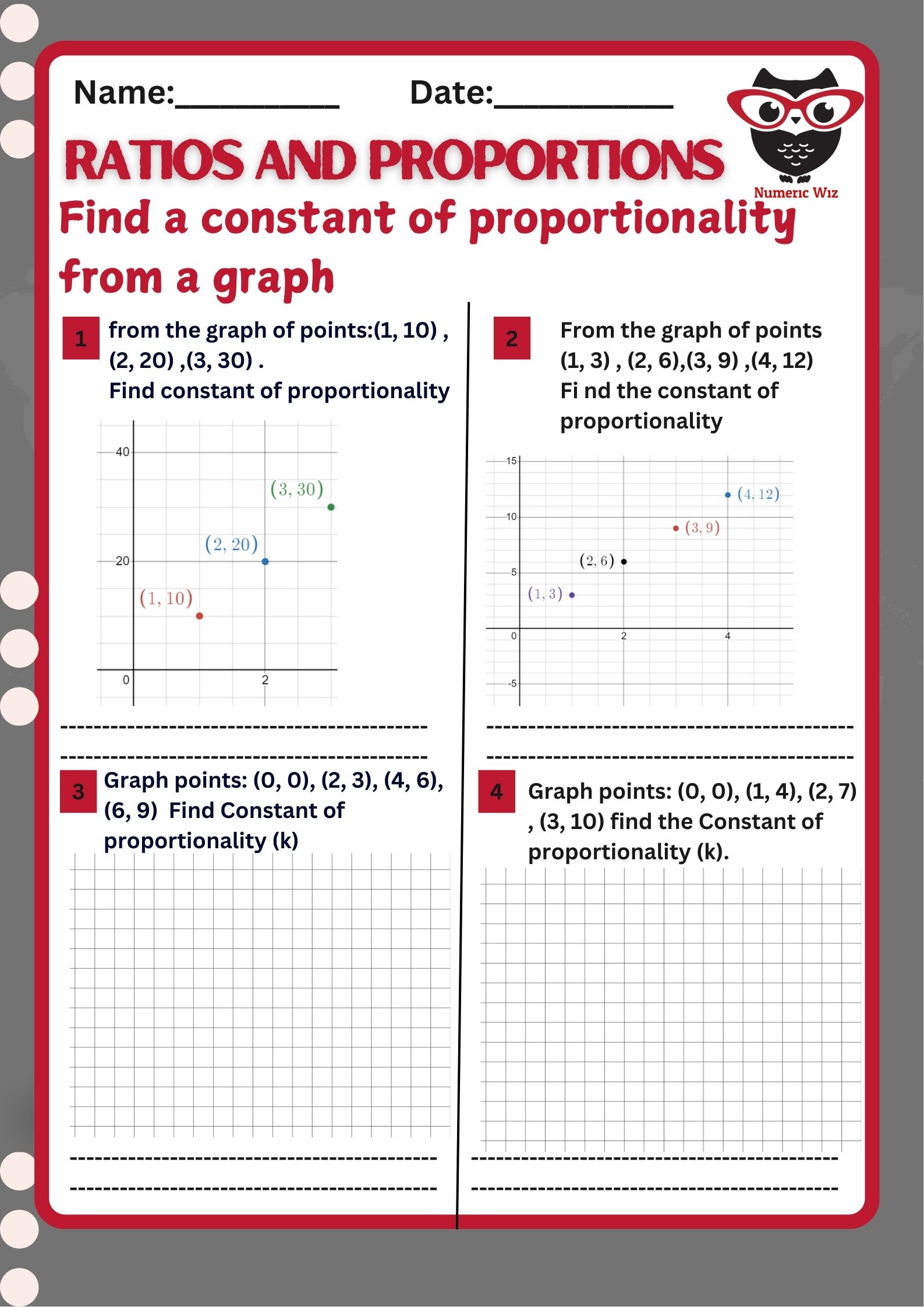
Identify proportional relationships from a graph.
Use the formula k = y / x to find the constant of proportionality.
Understand how graphs can visually confirm proportionality.
Connect math concepts with everyday ideas like cost per unit and distance per time.
This engaging worksheet helps students dive into one of the most important concepts in proportional relationships — the constant of proportionality (k). By using graphs and coordinate points, learners will practice finding the value of k, which tells us how two values are related in a consistent, proportional way.
Perfect for visual learners, this activity builds a strong foundation for working with equations like y = kx and understanding proportional patterns in real life.
How to read coordinate points from a graph.
How to calculate the constant of proportionality (k).
How to use the formula k = y / x (when y and x come from a proportional pair).
How to apply the concept of unit rate in a real graph-based setting.


Choose any point from the graph, e.g., (2, 20).
Use the formula:
k = y / x = 20 / 2 = 10
Check other points to confirm:
(1, 10) → 10 / 1 = 10
(3, 30) → 30 / 3 = 10
So, the constant of proportionality (k) = 10
Q2: Use points like (3, 9), (4, 12) from the graph. Apply the same method: k = y / x
Q3 & Q4: No graph given? No worries! The points are listed, so students must plot them or just plug into the formula.
The constant k is the same as the unit rate.
If you multiply x by k, you’ll always get y in a proportional relationship.
This is how many real-world problems — like price per item or speed — are solved using math!
 Great For:
Great For:Grade 7 ratio & proportion units
Visual learners who enjoy graphs
Strengthening skills before algebra
Homework, classwork, or math centers
Explore our Extraordinary Worksheets, Dive in and start solving today!
For a limited time
