Finding the Total Given a Part and a Percent

When working with percentages, one common problem is finding the total (or whole) when you are given a part of it and the percentage that part represents. This concept is widely used in real-life scenarios such as calculating total population based on a survey, determining original prices before discounts, and understanding financial growth.

To find the total, we use the formula:

(Percent / 100) × Total = Part

To solve for the total, the formula can be rearranged as:

Total = (Part × 100) / Percent

​Example 1:

Given: 30% of a number is 12. Find the total.

Total = 12 × 100 /30 = 40

Total = 40

Answer: 40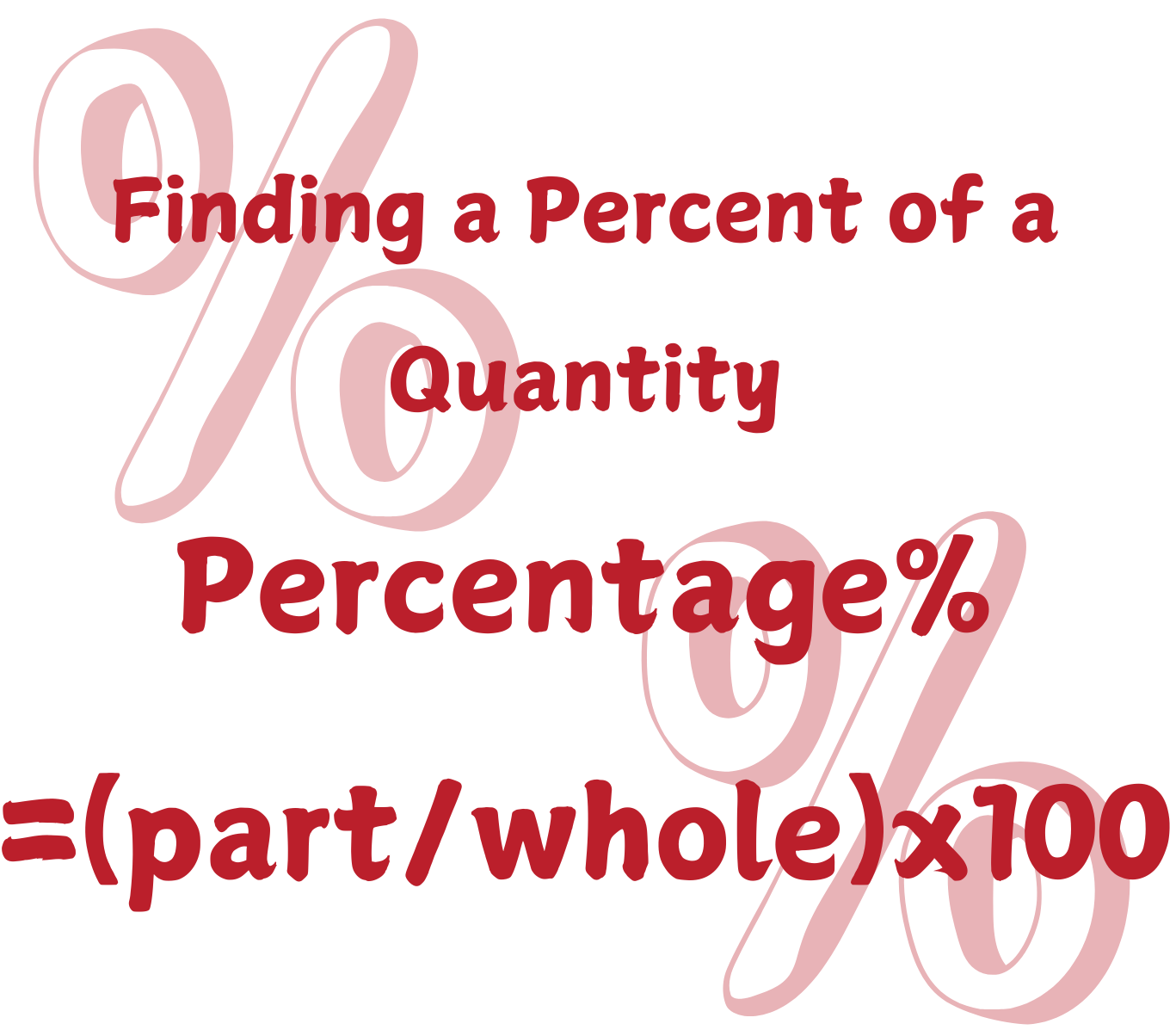

Example 2: Given: 20% of a number is 18. Find the total.

Total = 18 × 100 / 20= 90

Answer: 90

Example 3:

Given: 15% of a number is 9,000. Find the total.

Total = 9000 × 100 / 15

= 60,000

Answer: 60,000

Steps to Solve:

• Multiply the given part by 100.
• Divide the result by the given percentage.
• The final answer is the total.

Mastering this method helps in solving percentage-related problems quickly and accurately.

Applications in Real Life

Finding the total given a part and a percent is useful in various real-world situations, such as:

Calculating original prices before discounts or tax.

Estimating total populations based on sample data.

Determining overall expenses when given a percentage breakdown.

By mastering this skill, you can confidently solve problems related to finance, shopping, business, and data analysis.

Let's explore similar worksheets focused on calculating percentages and finding totals.