Recognize proportional relationships in algebraic equations
Understand the key structure of proportional equations: y = kx
Graph linear equations and interpret their visual meaning
Explain whether a relationship is proportional using both algebraic and graphical reasoning
Build connections between real-world situations and math models

Grade Level: 7
Standard: 7.RP.A.2a – Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
A proportional relationship is one where two quantities grow or shrink at the same constant rate. When graphed, this relationship creates a straight line that passes through the origin (0,0). In math terms, this is shown by the equation y = kx, where:
y is the dependent variable
x is the independent variable
k is the constant of proportionality (also called the unit rate)
This worksheet helps 7th-grade students understand how to analyze equations and their graphs to determine whether a relationship is proportional.
 Real-World Background Scenario
Real-World Background ScenarioImagine you're running a lemonade stand. You charge $2 per glass. So if you sell 1 glass, you earn $2. Sell 2 glasses, earn $4. This is a proportional relationship — your income grows at a constant rate of $2 per glass. Graph it, and the line passes right through the origin. That's exactly what we look for when deciding if equations are proportional!
Question: Is the equation y = 4x proportional?
Let’s analyze it step by step:
The equation y = 4x is in the form y = kx, where k = 4.
So far, so good!
Choose x-values: 0, 1, 2, 3
Now calculate y-values:
| x | y = 4x |
|---|---|
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
| 3 | 12 |
Plot the points (0,0), (1,4), (2,8), (3,12). You’ll see the line:
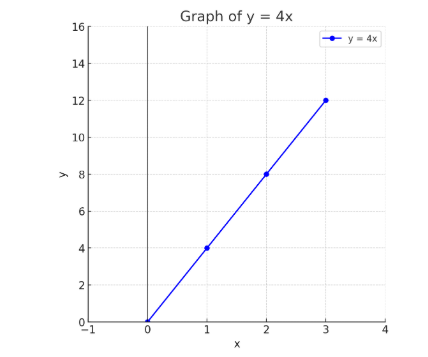
Goes through the origin and forms a straight line.
Yes, y = 4x is proportional because:
It's in the form y = kx
The graph is a straight line through the origin
Is y = 11x proportional?
Graph the equation and analyze: Is it in the form y = kx?
Does it pass through (0,0)?
(Spoiler: Yes, it’s proportional.)
Is y = 5 + 3x proportional?
Uh-oh! This one includes a constant (5).
Even though it forms a line, it doesn’t pass through the origin.
So, it's not proportional.

This worksheet is ideal for reinforcing graphing skills and deepening student's understanding of ratios, equations, and proportionality all while connecting algebra to real-world situations.
For a limited time
