Grade Level: 6–7 | Topic: Ratios & Proportions
Skill Focus: Analyzing Tables for Proportionality
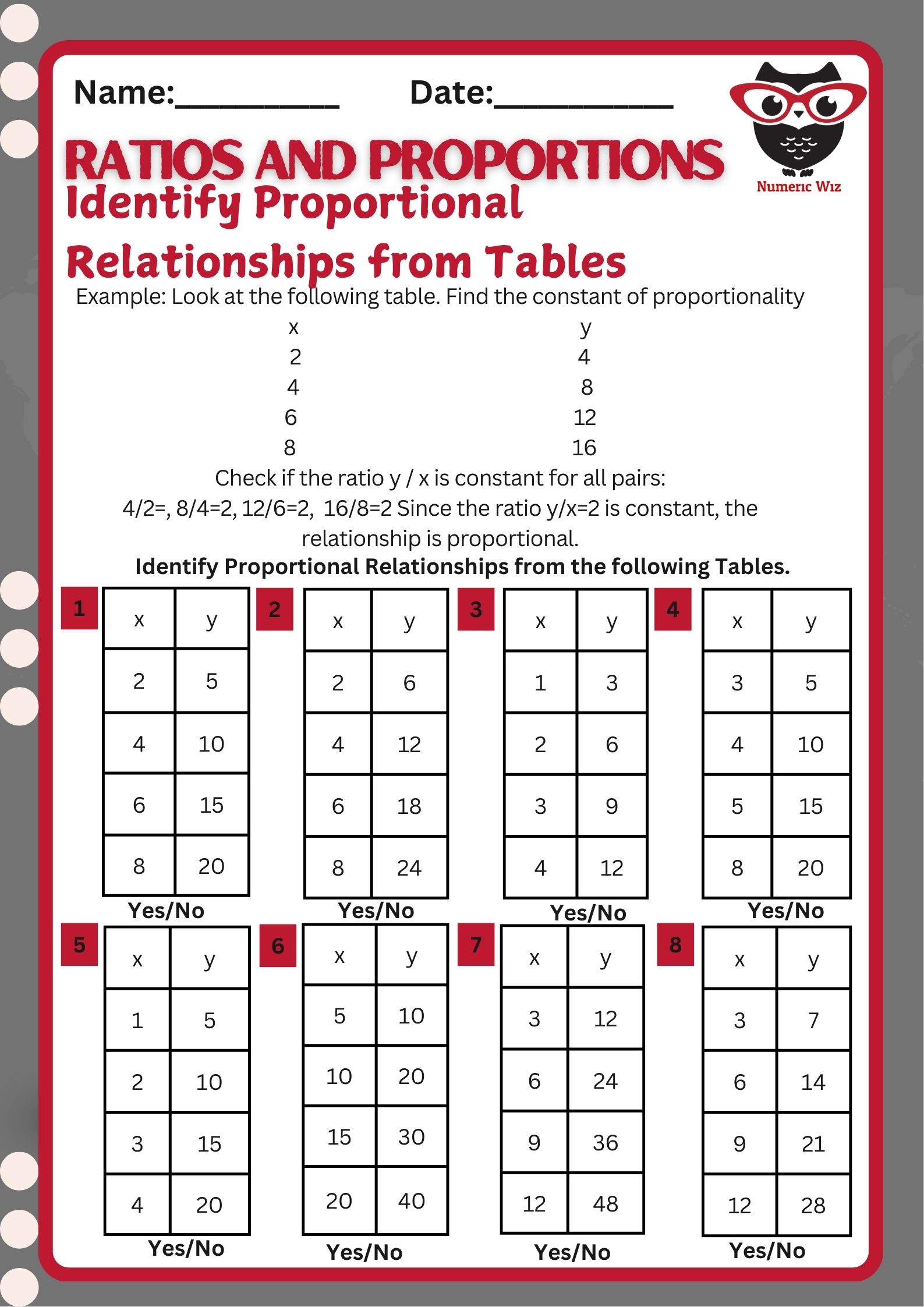
Understanding proportional relationships is essential in middle school math. This worksheet helps students determine whether two quantities in a table are proportional by checking for a constant ratio. If that ratio stays the same across all pairs, the relationship is proportional — simple as that!

Have you ever doubled a recipe? Or calculated how much money you’d make if you earned $10 per hour? Both are examples of proportional relationships. In math, when two quantities increase or decrease at the same rate, we say they’re proportional.
This worksheet is your chance to become a “Proportion Detective!” You’ll look at each table and decide:
Does the y-value always increase at the same rate as x?
Is the ratio y ÷ x (or x:y) the same every time?
Table:
| x | y |
|---|---|
| 2 | 4 |
| 4 | 8 |
| 6 | 12 |
| 8 | 16 |
Find the ratio y ÷ x for each row:
4 ÷ 2 = 2
8 ÷ 4 = 2
12 ÷ 6 = 2
16 ÷ 8 = 2
The ratio is the same (constant) each time: k = 2
Yes, the relationship is proportional.
This means y = 2x, a classic proportional equation!
Analyze tables of paired values.
Identify proportional relationships using consistent ratios.
Understand and explain the concept of the constant of proportionality (k).
Strengthen foundational skills needed for graphing and equations.

Imagine you’re buying apples — $3 for 1 pound. If you buy 2 pounds, it costs $6. Buy 3 pounds?
That’s $9.
The cost is directly proportional to the weight — and you’re using math from this very worksheet in the real world!
This worksheet is ideal for reinforcing graphing skills and deepening student's understanding of ratios, equations, and proportionality all while connecting algebra to real-world situations.
For a limited time
