Numbers are all around us, but not all numbers fit neatly into fractions or whole numbers. Some numbers, called irrational numbers, go on forever without repeating in their decimal form. Even though they can’t be written exactly as fractions, we can still approximate and locate them on a number line. Let’s explore how!
Irrational numbers cannot be written as a fraction (where both the numerator and denominator are integers). Their decimal expansions never end and never repeat.
π (pi) ≈ 3.141592653... (never-ending, non-repeating)
√2 ≈ 1.41421356...
√3 ≈ 1.7320508...
e (Euler’s number) ≈ 2.718281828...
Since these numbers don’t have exact decimal forms, we use rational approximations to find their location on a number line.
Even though irrational numbers don’t have exact locations, we can estimate their position using the following steps:
Step 1: Identify the Two Nearest Whole Numbers
Find two whole numbers that the irrational number falls between.
Number Line Representation:
(Blue line )(√5 ≈ 2.236)
Step 2: Use Decimal Approximations to Pinpoint the Location
Once we find the closest whole numbers, we refine our guess using a decimal approximation.
Example: Locate π on a number line.
We know π≈3.14, so it’s slightly past 3.1 but before 3.2.
Number Line Representation:
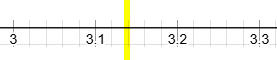
yellow line represents π≈3.14
Step 3: Divide the Number Line into Smaller Intervals
To be even more accurate, we divide sections into tenths or hundredths and mark our irrational number at its closest approximation.
Understanding how to estimate irrational numbers is more than just a math skill—it’s useful in the real world!
Architecture & Construction
Builders use square roots to measure diagonal distances (e.g., walls, ramps, and roofs).
Engineers use irrational numbers like √2 and π in designs.
Science & Physics
Scientists use π and e in formulas for waves, light, and motion.
Square roots help in calculating speed, acceleration, and energy.
GPS & Navigation
Satellite positioning systems rely on calculations involving irrational numbers to pinpoint exact locations on Earth.
Music & Sound
Sound waves and music frequencies involve irrational numbers (like the golden ratio).
By understanding how to place irrational numbers on a number line, we make sense of these endless, non-repeating decimals in a practical way.
Let’s explore and practice with the help of worksheets at NumericWiz!
For a limited time
