Topic Background: Understanding the Power of a Power Rule

In mathematics, exponents are a way to represent repeated multiplication. The Power of a Power Rule is one of the key laws of exponents. This rule states that when you raise a power to another power, you multiply the exponents:

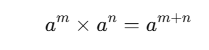
This rule is essential for simplifying expressions involving exponents, especially when dealing with large powers.

 Solved Examples

Let's apply the Power of a Power Rule to some examples:

Example 1:

Simplify     

Using the rule:

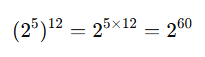
Example 2:

Simplify

Using the rule:

Example 3:

Simplify

Using the rule:

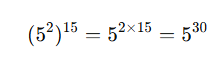
Step 2: Simplify → 

That’s it! Easy and fun — just multiply the powers.

 Fun Fact!

Did you know?

If you keep using the power of a power rule, numbers grow really fast. Just look at  and now try !

That’s the magic of exponential growth — the same mathbehind how fast rockets accelerate and how social media posts go viral!

Let's Get Started!

Ready to master the Power of a Power Rule? Dive into the worksheet and explore the fascinating world of exponents.

With practice, you'll simplify complex expressions with ease and confidence!

For a visual explanation, you might find this  helpful:

Click to Explore More