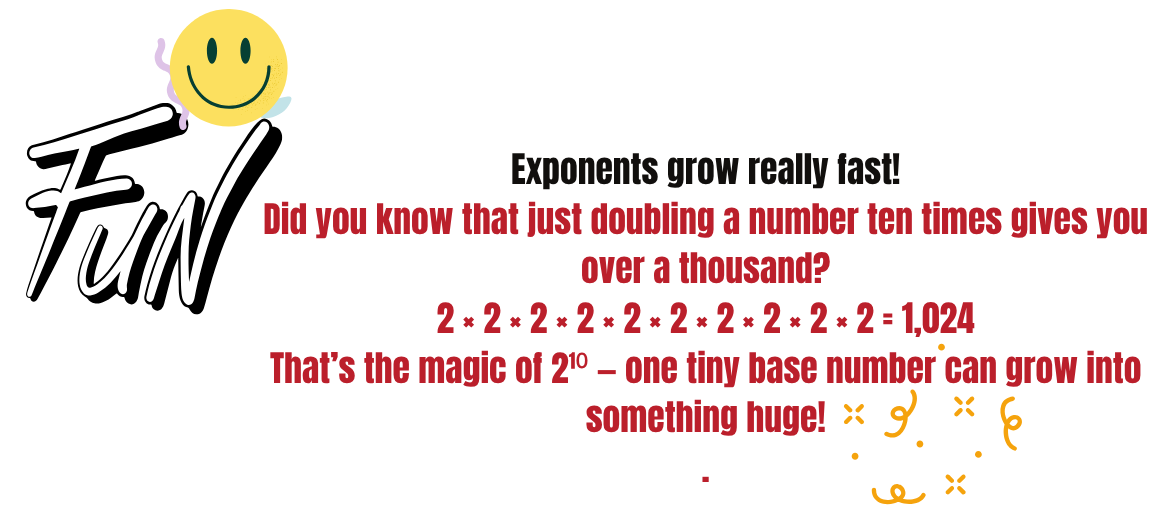Equivalent Expressions with Exponents

Why Students Struggle

Many students freeze when faced with exponents in algebraic expressions. This worksheet turns that confusion into clarity with the power of exponent rules. Designed to build confidence step by step, it helps students master simplifying expressions with exponents—one base and power at a time.

What Are Equivalent Expressions with Exponents?

Equivalent Expressions with Exponents is a strategy in algebra that teaches students how to simplify exponential expressions by applying laws such as the product rule, quotient rule, and power rule.

By recognizing patterns in repeated multiplication, students learn that expressions like:

2³ × 2² = 2⁵

This concept has developed from early arithmetic to advanced algebra, and today it forms a cornerstone of middle school and high school math.

Definition & Background

Equivalent expressions are algebraic statements that may appear different but simplify to the same value.

Example:

• x² × x³ = x⁵
  Both represent multiplying five x’s together.

Historically, the rules of exponents were formalized during the Renaissance, but their roots trace back to Babylonian and Greek number systems that used repeated multiplication in geometry. Today, exponent laws are essential tools in simplifying algebraic expressions, preparing students for higher-level math in polynomials, scientific notation, and exponential growth models.

Problem & Solution

Problem:
If Sara multiplies x⁴ × x², what is the simplified expression?

Solution:
(x⁴)(x²) = x⁴⁺² = x⁶

So, Sara ends up with x⁶.

Why Equivalent Exponent Expressions Matter

Have you ever looked at an exponential expression and wondered why it seems so complicated? The secret lies in applying the laws of exponents.

For example:

• x³ × x² = x⁵

This is not just a trick—it’s a fundamental skill that makes problem-solving faster and more accurate.

For 8th-grade math students, visual models make this concept clearer. Instead of memorizing rules, students can expand bases to see why:

• (x³)(x²) = x⁵

This bridges visual learning and abstract reasoning, aligning with Common Core standards 7.EE.A.1 and 8.EE.A.1, and prepares students for exponential functions, scientific notation, and real-world growth problems.

Common Core-Aligned Practice + Real-World Math

This worksheet aligns with 7.EE.A.1 and 8.EE.A.1. It provides 20+ practice problems, starting simple:

• 3² × 3³ = 3⁵

Then progresses to multi-step expressions involving both numbers and variables.

Step-by-Step Guide Using Exponent Laws

Step 1: Identify the Bases
Example: x⁴ × x³ → base is x.

Step 2: Apply the Product Rule
Add exponents when multiplying like bases.
x⁴ × x³ = x⁴⁺³ = x⁷

Step 3: Apply the Quotient Rule
Subtract exponents when dividing like bases.
x⁶ ÷ x² = x⁶⁻² = x⁴

Step 4: Apply the Power Rule
Multiply exponents when raising a power to a power.
(x³)² = x³×² = x⁶

Step 5: Simplify the Expression
Write the final simplified form.

Scaffolded Learning

Students don’t just jump into exponent rules—they build mastery gradually.

• Guided examples first

• Reduced hints later

• Independent practice with multi-step problems

Example progression:

1. (x²)(x³)

2. Simplify (2x³)² ÷ x⁴

Solved Examples

Example 1:
(x²)(x⁵) = x²⁺⁵ = x⁷

Example 2:
x⁶ ÷ x² = x⁶⁻² = x⁴

Example 3 (Power Rule):
(y³)² = y³×² = y⁶

Example 4 (Real-World):
A bacteria doubles every hour. After 3 hours: 2³. After 5 hours: 2⁵.
Growth after 8 hours: 2³ × 2⁵ = 2³⁺⁵ = 2⁸.

Conclusion: The population is 2⁸.

Real-World Applications of Exponents

• Population growth – exponential increases over time

• Finance – compound interest

• Science – scientific notation for very large/small numbers

• Technology – KB, MB, GB data storage

• Physics – energy, speed, scaling laws

Educator & Student Feedback

"I finally understood exponent rules! The step-by-step approach made it click."
– Ali R., 8th Grade Student

"My students used to dread exponents. With this worksheet, they see patterns and apply rules with confidence."
– Ms. Khan, Middle School Teacher

Final Challenge

Think you’ve cracked it?
Download the worksheet, solve it, and upload your answers to our “Evaluate Your Work” page. Our teachers will check it and send feedback just for you.